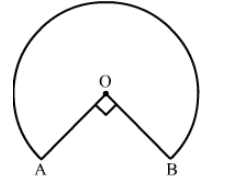
In the given figure, the shape of the top of a table is that of a sector of a circle with centre O and

We have $r=42 \mathrm{~cm}$ and $\theta=360^{\circ}-90^{\circ}=270^{\circ}$

Perimeter of the top of the table = Length of the major arc AB + Length of OA + Length of OB

$=\frac{\theta}{360^{\circ}} \times 2 \pi r+42+42$

$=\frac{270^{\circ}}{360^{\circ}} \times 2 \times \frac{22}{7} \times 42+84$

$=198+84$

$=282 \mathrm{~cm}$

Hence, the perimeter of the top of the table is 282 cm.