Question:
In the given figure the measure of $\angle \mathrm{D}$ and $\angle \mathrm{F}$ are respectively
(a) $50^{\circ}, 40^{\circ}$
(b) $20^{\circ}, 30^{\circ}$
(c) $40^{\circ}, 50^{\circ}$
(d) $30^{\circ}, 20^{\circ}$

Solution:
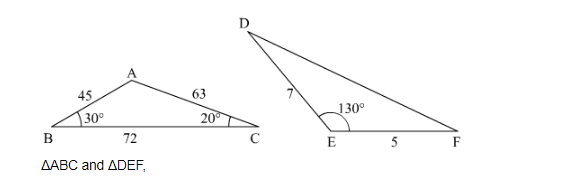
$\mathrm{ABAC}=\mathrm{EFED} \angle \mathrm{A}=\angle \mathrm{E}=130^{\circ}$
$\triangle \mathrm{ABC} \sim \triangle \mathrm{EFD} \quad$ (SAS Similarity)
$\triangle \mathrm{ABC} \sim \triangle \mathrm{EFD}$
$\therefore \angle \mathrm{F}=\angle \mathrm{B}=30^{\circ} \angle \mathrm{D}=\angle \mathrm{C}=20^{\circ}$
Hence the correct answer is (b)
