Question:
In the given figure, the chord AB of the larger of the two concentric circles, with centre O, touches the smaller circle at C. Prove that AC = CB.
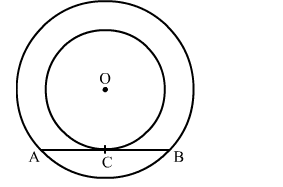
Solution:
Construction: Join OA, OC and OB
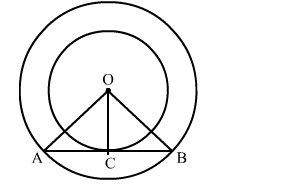
We know that the radius and tangent are perperpendular at their point of contact
∴ ∠OCA = ∠OCB = 90∘
Now, In △OCA and △OCB
∠OCA = ∠OCB = 90∘
OA = OB (Radii of the larger circle)
OC = OC (Common)
By RHS congruency
△OCA ≅ △OCB
∴ CA = CB
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.