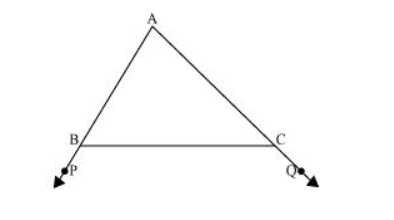
In the given figure sides AB and AC of ΔABC are extended to points P and Q respectively. Also, ∠PBC < ∠QCB. Show that AC > AB.

Solution:

In the given figure,

$\angle \mathrm{ABC}+\angle \mathrm{PBC}=180^{\circ}$ (Linear pair)

$\Rightarrow \angle \mathrm{ABC}=180^{\circ}-\angle \mathrm{PBC} \ldots(1)$

Also,

$\angle \mathrm{ACB}+\angle \mathrm{QCB}=180^{\circ}$

$\angle A C B=180^{\circ}-\angle Q C B \ldots(2)$

$\mathrm{As} \angle \mathrm{PBC}<\angle \mathrm{QCB}$ $\Rightarrow 180^{\circ}-\angle \mathrm{PBC}>180^{\circ}-\angle Q C B$

$\Rightarrow \angle A B C>\angle A C B$ [From equations (1) and (2)]

$\Rightarrow A C>A B$ (Side opposite to the larger angle is larger.)