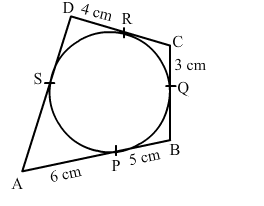
In the given figure, quadrilateral ABCD is circumscribed, touching the circle at P, Q, R and S.

(c) $36 \mathrm{~cm}$

Given, $A P=6 \mathrm{~cm}, B P=5 \mathrm{~cm}, C Q=3 \mathrm{~cm}$ and $D R=4 \mathrm{~cm} .$

$\mathrm{T}$ angents drawn from an external points to a circle are equal.

So, $\mathrm{AP}=\mathrm{AS}=6 \mathrm{~cm}, \mathrm{BP}=\mathrm{BQ}=5 \mathrm{~cm}, \mathrm{CQ}=\mathrm{CR}=3 \mathrm{~cm}, \mathrm{DR}=\mathrm{DS}=4 \mathrm{~cm} .$

$\therefore \mathrm{AB}=\mathrm{AP}+\mathrm{PB}=6+5=11 \mathrm{~cm}$

$\mathrm{BC}=\mathrm{BQ}+\mathrm{CQ}=5+3=8 \mathrm{~cm}$

$\mathrm{CD}=\mathrm{CR}+\mathrm{DR}=3+4=7 \mathrm{~cm}$

$\mathrm{AD}=\mathrm{AS}+\mathrm{DS}=6+4=10 \mathrm{~cm}$

$\therefore$ Pe rimeter of qua drilateral $\mathrm{ABCD}=\mathrm{AB}+\mathrm{BC}+\mathrm{CD}+\mathrm{DA}$

$=(11+8+7+10) \mathrm{cm}$

$=36 \mathrm{~cm}$