Question.
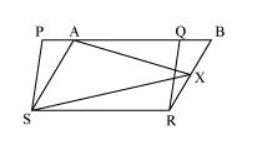
In the given figure, PQRS and ABRS are parallelograms and X is any point on side BR. Show that
(i) $\operatorname{ar}(\mathrm{PQRS})=\operatorname{ar}(\mathrm{ABRS})$
(ii) $\operatorname{ar}(A X S)=\frac{1}{2} \operatorname{ar}(P Q R S)$
(i) $\operatorname{ar}(\mathrm{PQRS})=\operatorname{ar}(\mathrm{ABRS})$
(ii) $\operatorname{ar}(A X S)=\frac{1}{2} \operatorname{ar}(P Q R S)$

Solution:
(i) It can be observed that parallelogram PQRS and ABRS lie on the same base SR
and also, these lie in between the same parallel lines SR and PB.
$\therefore$ Area $(P Q R S)=$ Area (ABRS) ... (1)
(ii) Consider $\triangle A X S$ and parallelogram $A B R S$.
As these lie on the same base and are between the same parallel lines $A S$ and $B R$,
$\therefore$ Area $(\triangle A X S)=\frac{1}{2}$ Area (ABRS) ... (2)
From equations (1) and (2), we obtain
Area $(\triangle A X S)=\frac{1}{2}$ Area $(P Q R S)$
(i) It can be observed that parallelogram PQRS and ABRS lie on the same base SR
and also, these lie in between the same parallel lines SR and PB.
$\therefore$ Area $(P Q R S)=$ Area (ABRS) ... (1)
(ii) Consider $\triangle A X S$ and parallelogram $A B R S$.
As these lie on the same base and are between the same parallel lines $A S$ and $B R$,
$\therefore$ Area $(\triangle A X S)=\frac{1}{2}$ Area (ABRS) ... (2)
From equations (1) and (2), we obtain
Area $(\triangle A X S)=\frac{1}{2}$ Area $(P Q R S)$
