In the given figure, PQ is a chord of a circle with centre O and PT is a tangent.

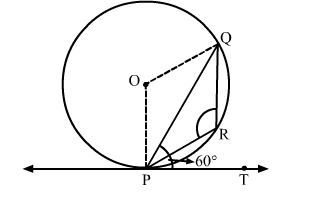
We know that the radius and tangent are perperpendular at their point of contact.
∴∠OPT = 90∘
Now, ∠OPQ = ∠OPT − ∠QPT = 90∘ − 60∘ = 30∘ 
Since, OP = OQ as both are radius
∴∠OPQ = ∠OQP = 30∘          (Angles opposite to equal sides are equal)
Now, In isosceles △POQ
∠POQ + ∠OPQ + ∠OQP = 180∘       (Angle sum property of a triangle)
⇒ ∠POQ = 180∘ − 30∘ − 30∘ = 120∘
Now, ∠POQ + reflex ∠POQ = 360∘         (Complete angle)
⇒ reflex ∠POQ = 360∘ − 120∘ = 240∘
We know that the angle subtended by an arc at the centre is double the angle subtended by the arc at any point on the remaining part of the circle.

$\therefore \angle \mathrm{PRQ}=\frac{1}{2}(\operatorname{reflex} \angle \mathrm{POQ})=120^{\circ}$