Question:
In the given figure, PQ and PR are tangents to a circle with centre A. If ∠QPA = 27∘ then ∠QAR equals
(a) 63∘
(b) 117∘
(c) 126∘
(d) 153∘
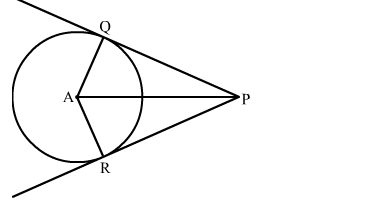
Solution:
We know that the radius and tangent are perperpendular at their point of contact
Now, In △PQA
∠PQA + ∠QAP + ∠APQ = 180∘ [Angle sum property of a triangle]
⇒ 90∘ + ∠QAP + 27∘ = 180∘ [∵∠OAB = ∠OBA ]
⇒ ∠QAP = 63∘
In △PQA and △PRA
PQ = PR (Tangents draw from same external point are equal)
QA = RA (Radii of the circle)
AP = AP (common)
By SSS congruency
△PQA ≅ △PRA
∠QAP = ∠RAP = 63∘
∴∠QAR = ∠QAP + ∠RAP = 63∘ + 63∘ = 126∘
Hence, the correct answer is option (c).
