Question:
In the given figure, PQ = 24, PR = 7 cm and O is the centre of the circle. Find the area of the shaded region.
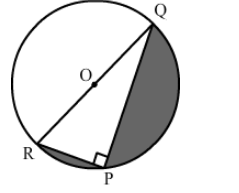
Solution:
In the right
$R Q=\sqrt{R P^{2}+P Q^{2}}$
$=\sqrt{7^{2}+24^{2}}$
$=\sqrt{49+576}$
$=25 \mathrm{~cm}$
OR = OQ = 12.5 cm
Now,
Area of the circle $=\pi r^{2}$
$=3.14 \times 12.5 \times 12.5$
$=490.625$ sq. $\mathrm{cm}$
Area of the semicircle $=\frac{490.625}{2}=245.31$ sq. $\mathrm{cm}$
Area of the triangle $=\frac{1}{2} \times b \times h=\frac{1}{2} \times 7 \times 24=84$ sq. $\mathrm{cm}$
Thus, we have:
Area of the shaded part = Area of the semicircle $-$ Area of the triangle
$=245.31-84$
$=161.31 \mathrm{~cm}^{2}$
