Question:
In the given figure, PA and PB are two tangents to the circle with centre O. If ∠APB = 60∘ then ∠OAB is
(a) 15∘
(b) 30∘
(c) 60∘
(d) 90∘
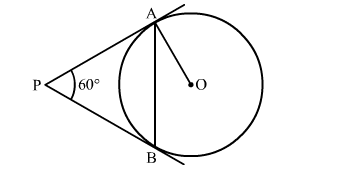
Solution:
Construction: Join OB
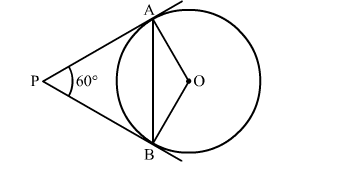
We know that the radius and tangent are perperpendular at their point of contact
∵∠OBP = ∠OAP = 90∘
Now, In quadrilateral AOBP
∠AOB + ∠OBP + ∠APB + ∠OAP = 360∘ [Angle sum property of a quadrilateral]
⇒ ∠AOB + 90∘ + 60∘ + 90∘ = 360∘
⇒ 240∘ + ∠AOB = 360∘
⇒ ∠AOB = 120∘
Now, In isoceles triangle AOB
∠AOB + ∠OAB + ∠OBA = 180∘ [Angle sum property of a triangle]
⇒ 120∘ + 2∠OAB = 180∘ [∵∠OAB = ∠OBA ]
⇒ ∠OAB = 30∘
Hence, the correct answer is option (b).
