In the given figure, PA and PB are two tangents from an external point P to a circle with centre O.

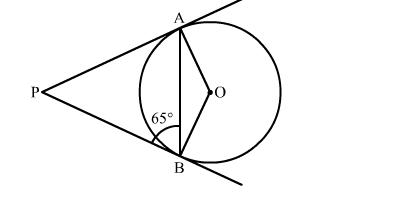
We know that tangents drawn from the external point are congruent.
∴ PA = PB
Now, In isoceles triangle APB
∠APB + ∠PBA + ∠PAB = 180∘            [Angle sum property of a triangle]
⇒ ∠APB + 65∘ + 65∘ = 180∘                          [∵∠PBA = ∠PAB = 65∘ ]
⇒ ∠APB = 50∘
We know that the radius and tangent are perperpendular at their point of contact
∴∠OBP = ∠OAP = 90∘
Now, In quadrilateral AOBP
∠AOB + ∠OBP + ∠APB + ∠OAP = 360∘           [Angle sum property of a quadrilateral]
⇒ ∠AOB + 90∘ + 50∘ + 90∘ = 360∘ 
⇒ 230∘ + ∠BOC = 360∘ 
⇒ ∠AOB = 130∘ 
Now, In isoceles triangle AOB
∠AOB + ∠OAB + ∠OBA = 180∘            [Angle sum property of a triangle]
⇒ 130∘ +  2∠OAB = 1800                          [∵∠OAB = ∠OBA ]
⇒ ∠OAB = 25∘