In the given figure, PA and PB are the tangents to a circle with centre O

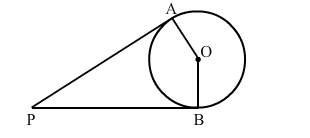
Here, $\mathrm{OA}=\mathrm{OB}$

And $\mathrm{OA} \perp \mathrm{AP}, \mathrm{OA} \perp \mathrm{BP}$ (Since tangents drawn from an external point are

perpendicular to the radius at the point of contact)

$\therefore \angle \mathrm{OAP}=90^{\circ}, \angle \mathrm{OBP}=90^{\circ}$

$\therefore \angle \mathrm{OAP}+\angle \mathrm{OBP}=90^{\circ}+90^{\circ}=180^{\circ}$

$\therefore \angle \mathrm{AOB}+\angle \mathrm{APB}=180^{\circ}\left(\right.$ S ince, $\left.\angle \mathrm{OAP}+\angle \mathrm{OBP}+\angle \mathrm{AOB}+\angle \mathrm{APB}=360^{\circ}\right)$

S um of opposite angle of a quadrilateral is $180^{\circ}$.

Hence, A, O, B and P are concyclic.