In the given figure, PA and PB are tangents to the circle drawn from an external point P.

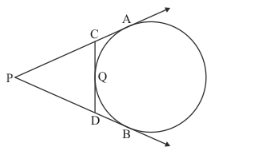
Solution:

Given data is as follows:

PB = 10 cm

CQ = 2 cm

We have to find the length of PC

We know that the length of two tangents drawn from the same external point will equal. Therefore,

PB = PA

It is given that PB = 10 cm

Therefore, PA = 10 cm

Also, from the same principle we have,

CQ = CA

It is given that CQ = 2 cm

Therefore, CA = 2cm

From the given figure we can say that,

PC = PA − CA

Now that we know the values of PA and CA, let us substitute the values in the above equation.

PC = 10 − 2

PC = 8 cm

Therefore, length of PC is 8 cm.