In the given figure, OQ : PQ = 3.4 and perimeter of Δ POQ = 60 cm.

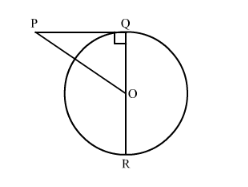
In the figure,

$\angle P Q O=90^{\circ}$. Therefore we can use Pythagoras theorem to find the side $P O$.

$P O^{2}=P Q^{2}+O Q^{2} \ldots \ldots(1)$

In the problem it is given that,

$\frac{O Q}{P Q}=\frac{3}{4}$

$O Q=\frac{3}{4} P Q$......(2)

Substituting this in equation (1), we have,

$P O^{2}=\frac{9 P Q^{2}}{16}+P Q^{2}$

$P O^{2}=\frac{25 P Q^{2}}{16}$

$P O=\sqrt{\frac{25 P Q^{2}}{16}}$

$P O=\frac{5}{4} P Q$  ........(3)

It is given that the perimeter of is 60 cm. Therefore,

PQ + OQ + PO = 60

Substituting (2) and (3) in the above equation, we have,

$P Q+\frac{3}{4} P Q+\frac{5}{4} P Q=60$

$\frac{12}{4} P Q=60$

$3 P Q=60$

$P Q=20$

Substituting for PQ in equation (2), we have,

$P O=\frac{5}{4} \times 15$

$O Q=\frac{3}{4} \times 20$

$O Q=15$

OQ is the radius of the circle and QR is the diameter. Therefore,

QR = 2OQ

QR = 30

Substituting for PQ in equation (3), we have,

$P O=\frac{5}{4} \times 20$

$P O=25$

Thus we have found that PQ = 20 cm, QR = 30 cm and PO = 25 cm.