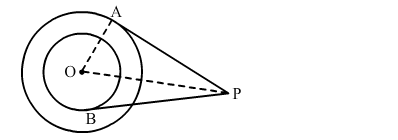
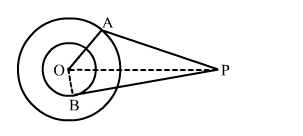
In the given figure, O is the centre of two concentric circles of radii 5 cm and 3 cm.

(c) $4 \sqrt{10} \mathrm{~cm}$

Given, $O P=5 \mathrm{~cm}, P A=12 \mathrm{~cm}$

Now, j oin $O$ and $B$.

Then, $O B=3 \mathrm{~cm}$.

Now, $\angle O A P=90^{\circ}$ (Tangents drawn from an external point are perpendicular

to the radius at the point of contact)

Now, in $\triangle O A P:$ :

$O P^{2}=O A^{2}+P A^{2}$

$\Rightarrow O P^{2}=5^{2}+12^{2}$

$\Rightarrow O P^{2}=25+144$

$\Rightarrow O P^{2}=169$

$\Rightarrow O P=\sqrt{169}$

$\Rightarrow O P=13$

Now, in $\triangle O B P$ :

$P B^{2}=O P^{2}-O B^{2}$

$\Rightarrow P B^{2}=13^{2}-3^{2}$

$\Rightarrow P B^{2}=169-9$

$\Rightarrow P B^{2}=160$

$\Rightarrow P B=\sqrt{160}$

$\Rightarrow P B=4 \sqrt{10} \mathrm{~cm}$