Question:
In the given figure, O is the centre of the circle. PA and PB are tangents. Show that AOBP is a cyclic quadrilateral
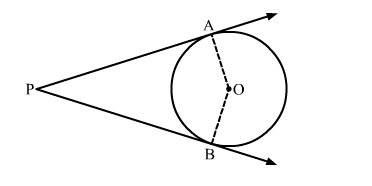
Solution:
We know that the radius and tangent are perpendicular at their point of contact
∵∠OBP = ∠OAP = 90∘
Now, In quadrilateral AOBP
∠APB + ∠AOB + ∠OBP + ∠OAP = 360∘ [Angle sum property of a quadrilateral]
⇒ ∠APB + ∠AOB + 90∘ + 90∘ = 360∘
⇒ ∠APB + ∠AOB = 180∘
Also, ∠OBP + ∠OAP = 180∘
Since, the sum of the opposite angles of the quadrilateral is 180∘
Hence, AOBP is a cyclic quadrilateral.
