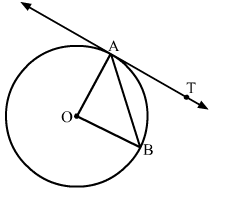
In the given figure, O is the centre of the circle AB is a chord and AT is the tangent at A.

Given: AO and BO are the radius of the circle
Since, AO = BO
∴ △AOB is an isosceles triangle.
Now, in △AOB
∠AOB + ∠OBA + ∠OAB = 180∘        (Angle sum property of triangle)
⇒ 100∘  + ∠OAB + ∠OAB = 180∘      (∠OBA = ∠OAB)
⇒ 2∠OAB = 80∘
⇒ ∠OAB = 40∘
We know that the radius and tangent are perperpendular at their point of contact
∵∠OAT = 90∘ 
⇒ ∠OAB  + ∠BAT = 90∘ 
⇒ ∠BAT = 90∘ − 40∘ = 50∘ 
Hence, the correct answer is option (b).