Question:
In the given figure, O is the centre of a circle in which ∠AOC = 100°. Side AB of quad. OABC has been produced to D. Then, ∠CBD = ?
(a) 50°
(b) 40°
(c) 25°
(d) 80°
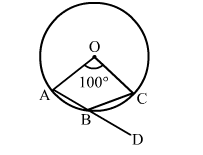
Solution:
(a) 50°
Take a point E on the remaining part of the circumference.
Join AE and CE.
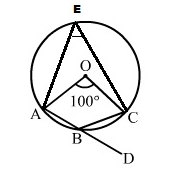
Then $\angle \mathrm{AEC}=\frac{1}{2} \angle \mathrm{AOC}=\left(\frac{1}{2} \times 100^{\circ}\right)=50^{\circ}$
Now, side AB of the cyclic quadrilateral ABCE has been produced to D.
∴ Exterior ∠CBD = ∠AEC = 50°
