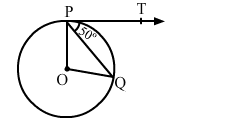
In the given figure, O is the centre of a circle and PT is the tangent to the circle.

(a) $100^{\circ}$

Given, $\angle Q P T=50^{\circ}$

and $\angle O P T=90^{\circ}$ (T angents drawn from an external point are perpendicular

to the radius at the point of contact)

$\therefore \angle O P Q=(\angle O P T-\angle Q P T)=\left(90^{0}-50^{0}\right)=40^{0}$

$O P=O Q(\mathrm{R}$ adius of the same circle $)$

$\Rightarrow \angle O Q P=\angle O P Q=40^{\circ}$

In $\Delta P O Q, \angle P O Q+\angle O Q P+\angle O P Q=180^{\circ}$

$\therefore \angle P O Q=180^{\circ}-\left(40^{0}+40^{0}\right)=100^{0}$