Question:
In the given figure, if AP = 10 cm, then BP =
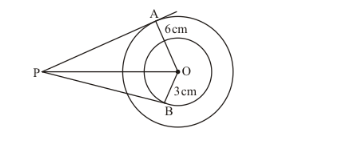
(a) $\sqrt{91} \mathrm{~cm}$
(b) $\sqrt{127} \mathrm{~cm}$
(c) $\sqrt{119} \mathrm{~cm}$
(d) $\sqrt{109} \mathrm{~cm}$
Solution:
Since the radius is always perpendicular to the tangent at the point of contact,
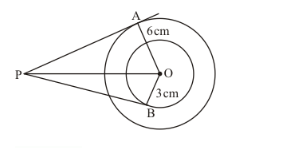
$\angle O A P=90^{\circ}$
Therefore,
$O P^{2}=O A^{2}+A P^{2}$
$O P^{2}=6^{2}+10^{2}$
$O P^{2}=36+100$
$O P^{2}=136$
$O P=\sqrt{136}$
Now, consider![]() . Here also, OB is perpendicular to PB since the radius will be perpendicular to the tangent at the point of contact. Therefore,
. Here also, OB is perpendicular to PB since the radius will be perpendicular to the tangent at the point of contact. Therefore,
$P B^{2}=O P^{2}-O B^{2}$
$P B^{2}=(\sqrt{136})^{2}-3^{2}$
$P B^{2}=136-9$
$P B^{2}=127$
$P B=\sqrt{127}$
The correct answer is option (b).
