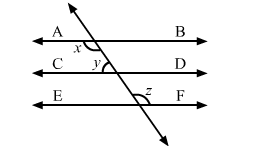
In the given figure, if AB || CD, CD || EF and y : z = 3 : 7, x = ?

Solution:

(b) 126°

Let $y=(3 a)^{\circ}$ and $z=(7 a)^{\circ}$

Let the transversal intersect AB at P, CD at O and EF at Q.

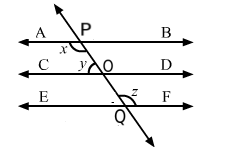
Then, we have:

$\angle C O P=\angle D O F=y \quad$ [Vertically-Opposite Angles]

$\therefore \angle O Q F+\angle D O Q=180^{\circ} \quad$ [Consecutive Interior Angles]

$\Rightarrow 3 a+7 a=180^{\circ}$

$\Rightarrow 10 a=180^{\circ}$

$\Rightarrow a=18^{\circ}$

$\therefore y=3 \times 18^{\circ}=54^{\circ}$

Also,

$\angle A P O+\angle C O P=180^{\circ}$

$\Rightarrow x+54^{\circ}=180^{\circ}$

$\Rightarrow x=126^{\circ}$