In the given figure, DE and DF are tangents from an external point D to a circle with centre A. If DE = 5 cm and DE ⊥ DF, then the radius of the circle is
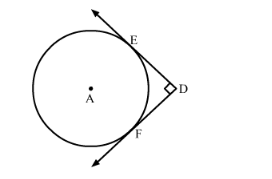
(a) 3 cm (b) 5 cm (c) 4 cm (d) 6 cm [CBSE 2013]
It is given that DE and DF are tangents from an external point D to a circle with centre A. DE = 5 cm and DE ⊥ DF.
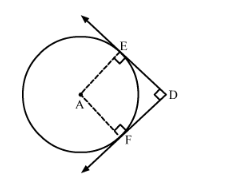
Join AE and AF.
Now, DE is a tangent at E and AE is the radius through the point of contact E.
$\therefore \angle \mathrm{AED}=90^{\circ} \quad$ (Tangent at any point of a circle is perpendicular to the radius through the point of contact)
Also, DF is a tangent at F and AF is the radius through the point of contact F.
$\therefore \angle \mathrm{AFD}=90^{\circ} \quad$ (Tangent at any point of a circle is perpendicular to the radius through the point of contact)
$\angle \mathrm{EDF}=90^{\circ} \quad(\mathrm{DE} \perp \mathrm{DF})$
Also, DF = DE (Lengths of tangents drawn from an external point to a circle are equal)
So, AEDF is a square.
∴ AE = AF = DE = 5 cm (Sides of square are equal)
Thus, the radius of the circle is 5 cm.
Hence, the correct answer is option B.
