In the given figure, CP and CQ are tangents from an external point C to a circle with centre O. AB is another tangent which touches the circle at R. If CP = 11 cm and BR = 4 cm, find the length of BC.
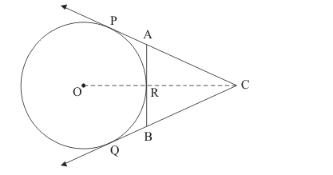
[Hint: We have, CP = 11 cm
∴ CP = CQ = CQ = 11 cm
Now, BR= BQ
⇒ BQ = 4 cm
∴ BC = CQ − BQ = (11−4)cm = 7 cm
We are given the following figure
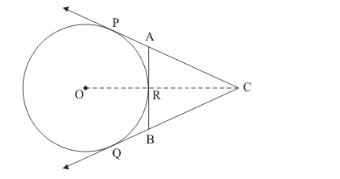
From the figure, we have
BC = CQ − BQ…… (1)
Let us now find out the values of CQ and BQ separately.
From the property of tangents we know that length of two tangents drawn from the same external point will be equal. Therefore,
CP = CQ
It is given in the problem that,
CP = 11
Therefore,
CQ = 11
Now let us find out the value of BQ.
Again from the same property of tangents, we know that length of two tangents drawn from the same external point will be equal. Therefore,
BR = BQ
It is given in the problem that,
BR = 4 cm
Therefore,
BQ = 4 cm
Now let us substitute the values of CQ and BQ in equation (1). We have,
BC = 11 − 4
BC = 7
Therefore, length of BC is 7 cm.
