Question:
In the given figure, bisectors AP and BQ of the alternate interior angles are parallel, then show that l ||m.

Solution:
Given, In the figure AP|| BQ, AP and BQ are the bisectors of alternate interior angles ∠CAB and ∠ABF.
To show l || m
Proof Since, AP|| BQ and t is transversal, therefore ∠PAB = ∠ABQ
[alternate interior angles]
=> 2 ∠PAB = 2 ∠ABQ [multiplying both sides by 2]
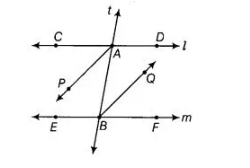
So, alternate interior angles are equal.
We know that, if two alternate interior angles are equal, then lines are parallel. Hence, l || m.
