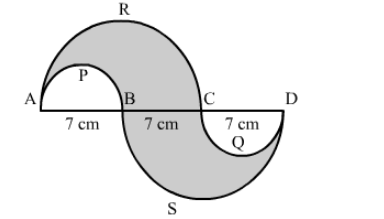
In the given figure, APB and CQD are semicircles of diameter 7 cm each,

Solution:

(i) Perimeter of shaded region = Length of the arc APB + Length of the arc ARC + Length of the arc BSD + Length of the arc CQD

$=\frac{1}{2} \times 2 \pi r_{1}+\frac{1}{2} \times 2 \pi r_{2}+\frac{1}{2} \times 2 \pi r_{3}+\frac{1}{2} \times 2 \pi r_{4}$

$=\frac{1}{2} \times 2 \pi\left(\frac{7}{2}\right)+\frac{1}{2} \times 2 \pi(7)+\frac{1}{2} \times 2 \pi(7)+\frac{1}{2} \times 2 \pi\left(\frac{7}{2}\right)$

$=2 \pi\left(\frac{7}{2}\right)+2 \pi(7)$

$=2 \pi\left(\frac{7}{2}+7\right)$

$=2 \times \frac{22}{7} \times \frac{21}{2}$

$=66 \mathrm{~cm}$

(ii) Area of shaded region = Area of the arc ARC + Area of the arc BSD − (Area of the arc APB + Area of the arc CQD)

$=\frac{1}{2} \times \pi\left(r_{1}\right)^{2}+\frac{1}{2} \times \pi\left(r_{2}\right)^{2}-\left[\frac{1}{2} \times \pi\left(\mathrm{r}_{3}\right)^{2}+\frac{1}{2} \times \pi\left(\mathrm{r}_{4}\right)^{2}\right]$

$=\frac{1}{2} \times \pi(7)^{2}+\frac{1}{2} \times \pi(7)^{2}-\left[\frac{1}{2} \times \pi\left(\frac{7}{2}\right)^{2}+\frac{1}{2} \times \pi\left(\frac{7}{2}\right)^{2}\right]$

$=\pi(7)^{2}-\pi\left(\frac{7}{2}\right)^{2}$

$=\pi\left(49-\frac{49}{4}\right)$

$=\frac{22}{7} \times \frac{147}{4}$

$=115.5 \mathrm{~cm}^{2}$