In the given figure, APB and AQO are semicircles and AO = OB.

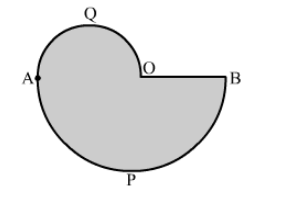
Permieter of shaded region = Length of the arc AQO + Length of the arc APB + Length of OB

$\Rightarrow 40=\frac{1}{2} \times 2 \pi\left(\frac{\mathrm{AO}}{2}\right)+\frac{1}{2} \times 2 \pi(\mathrm{OB})+\mathrm{OB}$

$\Rightarrow 40=\frac{11}{7} \mathrm{AO}+\frac{22}{7} \mathrm{OB}+\mathrm{OB}$

$\Rightarrow 40=\frac{11}{7} \mathrm{OB}+\frac{22}{7} \mathrm{OB}+\mathrm{OB} \quad[\because \mathrm{AO}=\mathrm{OB}]$

$\Rightarrow 40=\frac{40}{7} \mathrm{OB}$

$\Rightarrow \mathrm{OB}=7 \mathrm{~cm}$

Area of the shaded portion = Area of semicircle AQO + Area of semicircle APB

$=\frac{1}{2} \pi\left(\frac{7}{2}\right)^{2}+\frac{1}{2} \pi(7)^{2}$

$=\frac{1}{2} \times \frac{22}{7} \times\left(\frac{7}{2}\right)^{2}+\frac{1}{2} \times \frac{22}{7} \times(7)^{2}$

$=96.25 \mathrm{~cm}^{2}$

Hence, the area of the shaded portion is 96.25 cm2.