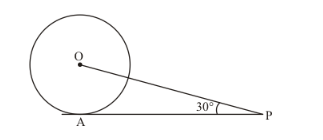
In the given figure, AP is a tangent to the circle with centre O such that OP = 4 cm and ∠OPA = 30°. Then, AP =

In the given figure,

if we join O and A, the line OA will be perpendicular to AP. This is because the radius of a circle will always be perpendicular to the tangent at the point of contact. Therefore, is a right triangle.

We know that,

$\cos \theta=\frac{\text { Adjacent side }}{\text { Hypotenuse }}$

$\cos \angle A P O=\frac{A P}{O P} \cdots \cdots$(1)

We know that, $\cos 30^{\circ}=\frac{\sqrt{3}}{2}$

$\cos \angle A P O=\frac{\sqrt{3}}{2}$.......(2)

From equations (1) and (2), we have,

$\frac{A P}{O P}=\frac{\sqrt{3}}{2}$

$A P=\frac{\sqrt{3}}{2} O P$

$A P=\frac{\sqrt{3}}{2} \times 4$

$A P=2 \sqrt{3}$

Therefore, option (c) is the correct answer.