In the given figure, $\angle X=62^{\circ}, \angle X Y Z=54^{\circ} .$ If $Y O$ and $Z O$ are the bisectors of $\angle X Y Z$ and $\angle X Z Y$ respectively of $\triangle X Y Z$, find $\angle O Z Y$ and $\angle Y O Z$.

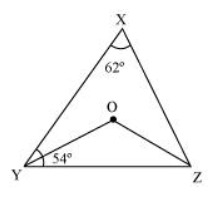
Solution:

As the sum of all interior angles of a triangle is $180^{\circ}$, therefore, for $\triangle X Y Z$,

$\angle X+\angle X Y Z+\angle X Z Y=180^{\circ}$

$62^{\circ}+54^{\circ}+\angle X Z Y=180^{\circ}$

$\angle X Z Y=180^{\circ}-116^{\circ}$

$\angle X Z Y=64^{\circ}$

$\angle O Z Y=\frac{64}{2}=32^{\circ}(O Z$ is the angle bisector of $\angle X Z Y)$

Similarly, $\angle O Y Z=\frac{54}{2}=27^{\circ}$

Using angle sum property for $\triangle O Y Z$, we obtain

$\angle O Y Z+\angle Y O Z+\angle O Z Y=180^{\circ}$

$27^{\circ}+\angle Y O Z+32^{\circ}=180^{\circ}$

$\angle Y O Z=180^{\circ}-59^{\circ}$

$\angle \mathrm{YOZ}=121^{\circ}$