In the given figure, an equilateral triangle has been inscribed in a circle of radius 4 cm.

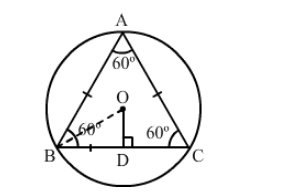
Draw $O D \perp B C$.

Because $\Delta A B C$ is equilateral, $\angle A=\angle B=\angle C=60^{\circ}$.

Thus, we have:

$\angle O B D=30^{\circ}$

$\Rightarrow \frac{O D}{O B}=\sin 30^{\circ}$

$\Rightarrow \frac{O D}{O B}=\frac{1}{2}$

$\Rightarrow O D=\left(\frac{1}{2} \times 4\right) \mathrm{cm} \quad[\because O B=$ radius $]$

$\Rightarrow O D=2 \mathrm{~cm}$

$\mathrm{BD}^{2}=\left(\mathrm{OB}^{2}-\mathrm{OD}^{2}\right) \quad[\mathrm{B} y$ Pythagoras' theorem $]$

$\Rightarrow \mathrm{BD}^{2}=\left(4^{2}-2^{2}\right) \mathrm{cm}^{2}$

$\Rightarrow \mathrm{BD}^{2}=(16-4) \mathrm{cm}^{2}$

$\Rightarrow \mathrm{BD}^{2}=12 \mathrm{~cm}^{2}$

$\Rightarrow \mathrm{BD}=2 \sqrt{3} \mathrm{~cm}$

Also,

$\mathrm{BC}=2 \times \mathrm{BD}$

$=(2 \times 2 \sqrt{3}) \mathrm{cm}$

$=4 \sqrt{3} \mathrm{~cm}$

$\therefore$ Area of the shaded region $=$ (Area of the circle) $-$ (Area of $\Delta A B C$ )

$=\left|(3.14 \times 4 \times 4)-\left(\frac{\sqrt{3}}{4} \times 4 \sqrt{3} \times 4 \sqrt{3}\right)\right| \mathrm{cm}^{2}$

$=|50.24-(12 \times 1.73)| \mathrm{cm}^{2}$

$=(50.24-20.76) \mathrm{cm}^{2}$

$=29.48 \mathrm{~cm}^{2}$