In the given figure, AM ⊥ BC and AN is the bisector of ∠A. If ∠ABC = 70° and ∠ACB = 20°, then ∠MAN = ?
Question:
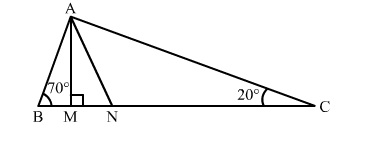
In the given figure, AM ⊥ BC and AN is the bisector of ∠A. If ∠ABC = 70° and ∠ACB = 20°, then ∠MAN = ?
Solution:
In $\Delta A B C$, we have:
$\angle A+\angle B+\angle C=180^{\circ} \quad$ [Sum of the angles of a triangle]
$\Rightarrow \angle A+70^{\circ}+20^{\circ}=180^{\circ}$
$\Rightarrow \angle A=90^{\circ}$
$\Rightarrow \frac{1}{2} \angle A=45^{\circ}$
$\Rightarrow \angle B A N=45^{\circ}$
$\ln \triangle A B M$, we have:
$\angle A B M+\angle A M B+\angle B A M=180^{\circ} \quad$ [Sum of the angles of a triangle]
$\Rightarrow 70^{\circ}+90^{\circ}+\angle B A M=180^{\circ}$
$\Rightarrow \angle B A M=20^{\circ}$
$\therefore \angle M A N=\angle B A N-\angle B A M$
$\Rightarrow \angle M A N=45^{\circ}-20^{\circ}$
$\Rightarrow \angle M A N=25^{\circ}$
