Question:
In the given figure, ABCD is a trapezium of area 24.5 cm2 , If AD || BC, ∠DAB = 90°, AD = 10 cm, BC = 4 cm and ABE is quadrant of a circle, then find the area of the shaded region.
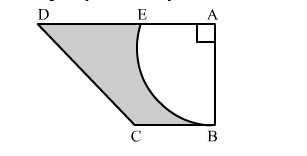
Solution:
Area of trapezium $=\frac{1}{2}(\mathrm{AD}+\mathrm{BC}) \times \mathrm{AB}$
$\Rightarrow 24.5=\frac{1}{2}(10+4) \times \mathrm{AB}$
$\Rightarrow \mathrm{AB}=3.5 \mathrm{~cm}$
Area of shaded region = Area of trapezium ABCD − Area of quadrant ABE
$=24.5-\frac{1}{4} \pi(\mathrm{AB})^{2}$
$=24.5-\frac{1}{4} \times \frac{22}{7}(3.5)^{2}$
$=24.5-9.625$
$=14.875 \mathrm{~cm}^{2}$
Hence, the area of shaded region is 14.875 cm2
