In the given figure, ABCD is a square of side 4 cm. A quadrant of a circle of radius 1 cm is drawn at each vertex of the square and a circle of diameter 2 cm is also drawn. Find the area of the shaded region.
[Use $\pi=3.14 .$ ]
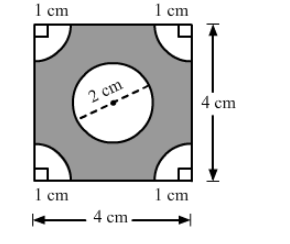
Area of the square $A B C D=(\text { Side })^{2}$
$=4^{2}$
$=16 \mathrm{~cm}^{2}$
Area of the circle $=\pi r^{2}$
Radius = 1 cm
Area $=3.14 \times(1)^{2}$
$=3.14 \mathrm{~cm}^{2}$
Area of the quadrant of one circle $=\frac{1}{4} \pi r^{2}$
$=\frac{1}{4} \times 3.14 \times 1^{2}$
$=0.785 \mathrm{~cm}^{2}$
Area of the quadrants of four circles $=0.785 \times 4=3.14 \mathrm{~cm}^{2}$
Area of the shaded region = Area of the square
$=16-3.14-3.14=9.72 \mathrm{~cm}^{2}$
