Question:
In the given figure, ABCD is a square each of whose sides measures 28 cm. Find the area of the shaded region.
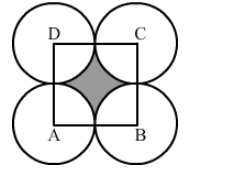
Solution:
Let r be the radius of the circle.
Thus, we have:
$r=\frac{28}{2} \mathrm{~cm}$
$=14 \mathrm{~cm}$
Now,
Area of the shaded region $=$ (Area of the square $A B C D$ ) $-4$ (Area of the sector where $r=14 \mathrm{~cm}$ and $\theta=90^{\circ}$ )
$=\left|(28 \times 28)-4\left(\frac{22}{7} \times 14 \times 14 \times \frac{90}{360}\right)\right| \mathrm{cm}^{2}$
$=|784-4(154)| \mathrm{cm}^{2}$
$=(784-616) \mathrm{cm}^{2}$
$=168 \mathrm{~cm}^{2}$
