In the given figure, ABCD is a square and ∠PQR = 90°. If PB = QC = DR, prove that

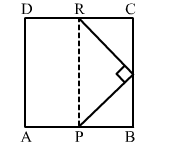
Given: ABCD is a square and ∠PQR = 90°.
Also, PB = QC = DR

(i) We have:
  BC = CD                (Sides of square)
  CQ = DR                   (Given)
  BC = BQ + CQ
⇒ CQ = BC − BQ
∴ DR = BC − BQ           ...(i)
   
Also, CD = RC+ DR
∴ DR = CD −  RC = BC − RC            ...(ii)
From (i) and (ii), we have:
BC − BQ = ​BC − RC
∴ BQ = RC

(ii) In ∆RCQ and ∆QBP, we have:
PB = QC   (Given)
BQ = RC  (Proven above)
∠RCQ = ∠QBP   (90o each)
i.e., ∆RCQ ≅ ∆QBP       (SAS congruence rule)
∴ QR =  PQ                (By CPCT)

(iii) ∆RCQ ≅ ∆QBP and QR = PQ (Proven above)

$\therefore \ln \triangle \mathrm{RPQ}, \angle \mathrm{QPR}=\angle \mathrm{QRP}=\frac{1}{2}\left(180^{\circ}-90^{\circ}\right)=\frac{90^{\circ}}{2}=45^{\circ}$