In the given figure, ABCD is a rectangle with AB = 80 cm and BC = 70 cm,

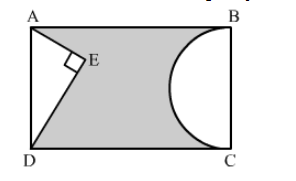
We know that the opposite sides of a rectangle are equal
AD = BC =  70 cm
In right triangle AED
AE2 = AD2 − DE2  
= (70)2 − (42)2 
= 4900 − 1764
= 3136
∴ AE2 = 3136
⇒ AE = 56
= Area of the shaded region = Area of rectangle − (Area of triangle  AED + Area of semicircle)

$=\mathrm{AB} \times \mathrm{BC}-\left[\frac{1}{2} \times \mathrm{AE} \times \mathrm{DE}+\frac{1}{2} \pi\left(\frac{\mathrm{BC}}{2}\right)^{2}\right]$

$=80 \times 70-\left[\frac{1}{2} \times 56 \times 42+\frac{1}{2} \times \frac{22}{7}\left(\frac{70}{2}\right)^{2}\right]$

$=5600-3101$

$=2499 \mathrm{~cm}^{2}$

Hence, the area of shaded region is 2499 cm2