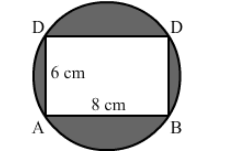
In the given figure, ABCD is a rectangle inscribed in a circle having length 8 cm and breadth 6 cm.

All options are incorrect; the correct answer is 30.5 cm.

Join AC.
Now, AC is the diameter of the circle.

We have :

$A C^{2}=A B^{2}+B C^{2} \quad[$ By Pythagoras' theorem $]$

$\Rightarrow A C^{2}=\left\{(8)^{2}+(6)^{2}\right\} \mathrm{cm}^{2}$

$\Rightarrow A C^{2}=(64+36) \mathrm{cm}^{2}$

$\Rightarrow A C^{2}=100 \mathrm{~cm}^{2}$

$\Rightarrow A C=10 \mathrm{~cm}$

$\therefore$ Radius of the circle $=\frac{10}{2} \mathrm{~cm}$

$=5 \mathrm{~cm}$

Now,
Area of the shaded region = Area of the circle with radius 5 cm -">−Area of the rectangle ABCD

$=|(3.14 \times 5 \times 5)-(8 \times 6)| \mathrm{cm}^{2}$

$=\left|\left(\frac{314}{100} \times 25\right)-48\right| \mathrm{cm}^{2}$

$=\left(\frac{157}{2}-48\right) \mathrm{cm}^{2}$

$=\frac{61}{2} \mathrm{~cm}^{2}$

$=30.5 \mathrm{~cm}^{2}$