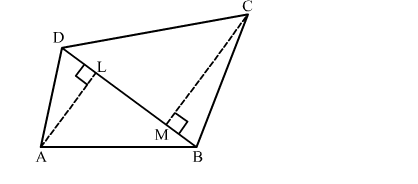
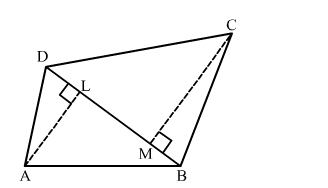
In the given figure, ABCD is a quadrilateral in which diagonal BD = 24 cm, AL ⊥ BD and CM ⊥ BD such that AL = 9 cm and CM = 12 cm.

We have,

$\mathrm{BD}=24 \mathrm{~cm}, \mathrm{AL}=9 \mathrm{~cm}, \mathrm{CM}=12 \mathrm{~cm}, \mathrm{AL} \perp \mathrm{BD}$ and $\mathrm{CM} \perp \mathrm{BD}$

Area of the quadrilateral $=\operatorname{ar}(\Delta \mathrm{ABD})+\operatorname{ar}(\Delta \mathrm{BCD})$

$=\frac{1}{2} \times \mathrm{BD} \times \mathrm{AL}+\frac{1}{2} \times \mathrm{BD} \times \mathrm{CM}$

$=\frac{1}{2} \times 24 \times 9+\frac{1}{2} \times 24 \times 12$

$=108+144$

$=252 \mathrm{~cm}^{2}$

So, the area of the quadrilateral ABCD is 252 cm2.