Question:
In the given figure, ABCD is a || gm in which diagonals AC and BD intersect at O. If ar(||gm ABCD) is 52 cm2, then the ar(∆OAB) = ?
(a) $26 \mathrm{~cm}^{2}$
(b) $18.5 \mathrm{~cm}^{2}$
(c) $39 \mathrm{~cm}^{2}$
(d) $13 \mathrm{~cm}^{2}$
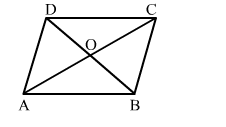
Solution:
(d) $13 \mathrm{~cm}^{2}$
The diagonals of a parallelogram divides it into four triangles of equal areas.
$\therefore$ Area of $\Delta O A B=\frac{1}{4} \times \operatorname{ar}(\| \mathrm{gm} A B C D)$
$\Rightarrow \operatorname{ar}(\Delta O A B)=\frac{1}{4} \times 52=13 \mathrm{~cm}^{2}$
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.