Question:
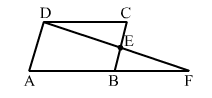
In the given figure, ABCD is a || gm and E is the mid-point of BC. Also, DE and AB when produced meet at F. Then,
(a) $A F=\frac{3}{2} A B$
(b) $A F=2 A B$
(c) $A F=3 A B$
(d) $A F^{2}=2 A B^{2}$
Solution:
(b) AF = 2 AB
Explanation:
In parallelogram ABCD, we have:
AB || DC
∠DCE = ∠ EBF (Alternate interior angles)
In ∆ DCE and ∆ BFE, we have:
∠DCE = ∠ EBF (Proved above)
∠DEC = ∠ BEF (Vertically opposite angles)
BE = CE ( Given)
i.e., ∆ DCE ≅ ∆ BFE (By ASA congruence rule)
∴ DC = BF (CPCT)
But DC= AB, as ABCD is a parallelogram.
∴ DC = AB = BF ...(i)
Now, AF = AB + BF ...(ii)
From (i), we get:
∴ AF = AB + AB = 2AB
BE = CE ( Given)
i.e., ∆ DCE ≅ ∆ BFE (By ASA congruence rule)
∴ DC = BF (CPCT)
But DC= AB, as ABCD is a parallelogram.
∴ DC = AB = BF ...(i)
Now, AF = AB + BF ...(ii)
From (i), we get:
∴ AF = AB + AB = 2AB
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.