In the given figure, ∆ABC is right-angled at A.

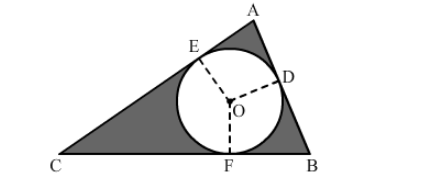
Using Pythagoras' theorem for triangle ABC, we have:

$C A^{2}+A B^{2}=B C^{2}$

$C A=\sqrt{B C^{2}-A B^{2}}$

$=\sqrt{100-36}$

$=\sqrt{64}$

$=8 \mathrm{~cm}$

Now, we must find the radius of the incircle. Draw OE, OD and OF perpendicular to AC, AB and BC, respectively.

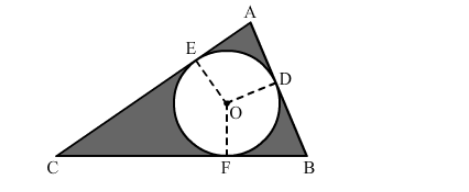
Consider quadrilateral AEOD.
Here,

$E O=O D$ (Both are radii.)

Because the circle is an incircle, AE and AD are tangents to the circle.

$\angle A E O=\angle A D O=90^{\circ}$

Also,

$\angle A=90^{\circ}$

Therefore, AEOD is a square.

Thus, we can say that $A E=E O=O D=A D=r$.

$C E=C F=8-r$

$B F=B D=6-r$

$C F+B F=10$

$\Rightarrow(8-r)+(6-r)=10$

$\Rightarrow 14-2 r=10$

$\Rightarrow r=2 \mathrm{~cm}$

Area of the shaded part = Area of the triangle -">−Area of the circle

$=\left\{\frac{1}{2} \times 6 \times 8\right\}-\{\pi \times 2 \times 2\}$

$=24-12.56$

$=11.44 \mathrm{~cm}^{2}$