In the given figure, AB is a diameter of a circle with centre O and DO || CB.

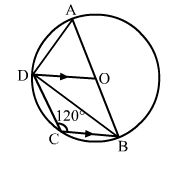
We have,
AB is a diameter of the circle where O is the centre, DO || BC and ∠BCD = 120°.
(i)
Since ABCD is a cyclic quadrilateral, we have:
∠BCD + ∠BAD = 180°
⇒ 120° + ∠BAD = 180°
⇒ ∠BAD = (180° – 120°) = 60°
∴ ∠BAD = 60°
(ii)
∠BDA = 90° (Angle in a semicircle)
In Δ ABD, we have:
∠BDA + ∠BAD + ∠ABD = 180°
⇒ 90° + 60° + ∠ABD = 180°
⇒ ∠ABD = (180° – 150°) = 30°
∴ ∠ABD = 30°
(iii)
OD = OA (Radii of a circle)
∠ODA = ∠OAD
 = ∠BAD = 60°
∠ODB = 90° - ∠ODA = (90° - 60°) = 30°
Here, DO || BC (Given; alternate angles)
∠CBD = ∠ODB = 30°
∴ ∠CBD = 30°
(iv)
∠ADC = ∠ADB + ∠CDB
= 90° + 30° = 120°
In ΔAOD, we have:
∠ODA + ∠OAD +∠AOD = 180°
⇒ 60° + 60° + ∠AOD = 180°
⇒ ∠AOD = 180° – 120° = 60°

Since all the angles of ΔAOD are of 60° each, ΔAOD is an equilateral triangle.