In the given figure, AB || CD. Find the value of x.

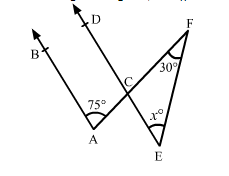
Solution:

$A B \| C D$ and $A C$ is the transversal.

Then,

$\angle B A C+\angle A C D=180^{\circ} \quad[$ Consecutive Interior Angles $]$

$\Rightarrow 75+\angle A C D=180$

$\Rightarrow \angle A C D=105^{\circ}$

And,

$\angle A C D=\angle E C F \quad[$ Vertically-Opposite Angles $]$

$\Rightarrow \angle E C F=105^{\circ}$

We know that the sum of the angles of a triangle is 180°">180°180°.

$\angle E C F+\angle C F E+\angle C E F=180^{\circ}$

$\Rightarrow 105^{\circ}+30^{\circ}+x=180^{\circ}$

$\Rightarrow 135^{\circ}+x=180^{\circ}$

$\Rightarrow x=45^{\circ}$