In the given figure, a circle inscribed in a triangle ABC, touches the sides AB, BC and AC at point D,
Question:
In the given figure, a circle inscribed in a triangle ABC, touches the sides AB, BC and AC at point D, E and F respectively. If AB = 14 cm, BC = 8 cm and AC = 12 cm. Find the lengths of AD, BE and CF
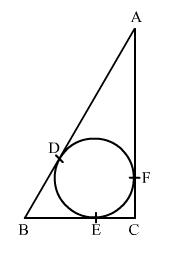
Solution:
We know that tangent segments to a circle from the same external point are congruent.
Now, we have
AD = AF, BD = BE and CE = CF
Now, AD + BD = 14 cm .....(1)
AF + FC = 12 cm
⇒ AD + FC = 12 cm .....(2)
BE + EC = 8 cm
⇒ BD + FC = 8 cm .....(3)
Adding all these we get
AD + BD + AD + FC + BD + FC = 34
⇒2(AD + BD + FC) = 34
⇒AD + BD + FC = 17 cm .....(4)
Solving (1) and (4), we get
FC = 3 cm
Solving (2) and (4), we get
BD = 5 cm = BE
Solving (3) and (4), we get
and AD = 9 cm
