In the given figure, $A C=A E, A B=A D$ and $\angle B A D=\angle E A C$. Show that $B C=D E$.

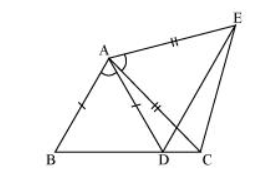
Solution:

It is given that $\angle B A D=\angle E A C$

$\angle B A D+\angle D A C=\angle E A C+\angle D A C$

$\angle B A C=\angle D A E$

In $\triangle B A C$ and $\triangle D A E$,

$\mathrm{AB}=\mathrm{AD}$ (Given)

$\angle B A C=\angle D A E($ Proved above $)$

$\mathrm{AC}=\mathrm{AE}$ (Given)

$\therefore \triangle \mathrm{BAC} \cong \triangle \mathrm{DAE}($ By $S A S$ congruence rule $)$

$\therefore \mathrm{BC}=\mathrm{DE}(\mathrm{By} \mathrm{CPCT})$