Question:
In the given figure,
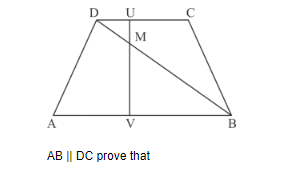
(i) $\triangle \mathrm{DMU} \sim \triangle \mathrm{BMV}$
(ii) $\mathrm{DM} \times \mathrm{BV}=\mathrm{BM} \times \mathrm{DU}$
Solution:
(i) Given $A B \| D C$
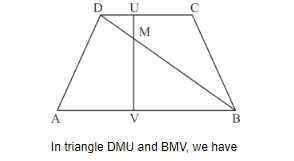
$\angle M U D=\angle M V B$
Each angle is equal to $90^{\circ}$
$\angle U M D=\angle V M B$
Each are vertically opposite angles.
Therefore, by AA-criterion of similarity $\triangle D M U \sim \triangle B M V$
(ii)Since $\triangle D M U \sim \triangle B M V$
$\frac{D M}{B M}=\frac{M U}{M V}=\frac{D U}{B V}$
$\frac{D M}{B M}=\frac{D U}{B V}$
By cross multiplication, we get $D M \times B V=D U \times B M$
Hence proved that $D M \times B V=D U \times B M$
