In the given figure,

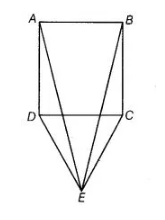
Given in figure $\triangle C D E$ is an equilateral triangle formed on a side $C D$ of a square $A B C D$.

To show $\triangle \mathrm{ADE} \cong \triangle B C E$

Proof $\ln \triangle A D E$ and $\triangle B C E$,   $D E=C E$    [sides of an equilateral triangle]

$\angle A D E=\angle B C E$

$\left[\begin{array}{l}\because \angle A D C=\angle B C D=90^{\circ} \text { and } \angle E D C=\angle E C D=60^{\circ} \\ \therefore \angle A D E=90^{\circ}+60^{\circ}=150^{\circ} \text { and } \angle B C E=90^{\circ}+60^{\circ}=150^{\circ}\end{array}\right]$

and $A D=B C$ [sides of a square]

$\therefore$ $\triangle A D E \cong \triangle B C E$ [by SAS congruence rule]