Question.
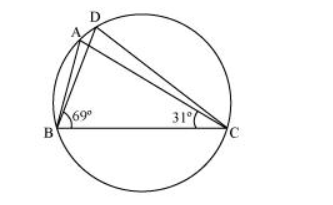
In the given figure, $\angle A B C=69^{\circ}, \angle A C B=31^{\circ}$, find $\angle B D C$.
Solution:
In $\triangle A B C$
$\angle B A C+\angle A B C+\angle A C B=180^{\circ}$ (Angle sum property of a triangle)
$\Rightarrow \angle B A C+69^{\circ}+31^{\circ}=180^{\circ}$
$\Rightarrow \angle B A C=180^{\circ}-100^{\circ}$
$\Rightarrow \angle B A C=80^{\circ}$
$\angle B D C=\angle B A C=80^{\circ}$ (Angles in the same segment of a circle are equal)
In $\triangle A B C$
$\angle B A C+\angle A B C+\angle A C B=180^{\circ}$ (Angle sum property of a triangle)
$\Rightarrow \angle B A C+69^{\circ}+31^{\circ}=180^{\circ}$
$\Rightarrow \angle B A C=180^{\circ}-100^{\circ}$
$\Rightarrow \angle B A C=80^{\circ}$
$\angle B D C=\angle B A C=80^{\circ}$ (Angles in the same segment of a circle are equal)
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.