In the following figure, shows a kite in which BCD is the shape of

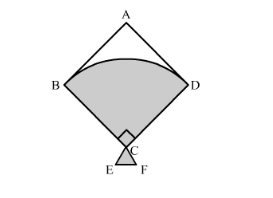
We will find the area of the shaded region as shown below,

Area of the shaded region = area of quadrant + area of isosceles triangle ……..(1)

$\therefore$ Area of shaded region $=\frac{90}{360} \times \pi \times 42^{2}+\frac{1}{2} \times 6 \times 6$

$\therefore$ Area of shaded region $=\frac{1}{4} \times \pi \times 42^{2}+\frac{1}{2} \times 36$

Substituting $\pi=\frac{22}{7}$ we get,

$\therefore$ Area of shaded region $=\frac{1}{4} \times \frac{22}{7} \times 42^{2}+\frac{1}{2} \times 36$

$\therefore$ Area of shaded region $=\frac{1}{2} \times 11 \times 6 \times 42+18$

$\therefore$ Area of shaded region $=11 \times 3 \times 42+18$

$\therefore$ Area of shaded region $=1386+18$

$\therefore$ Area of shaded region $=1404$

Therefore, area of the shaded region is $1404 \mathrm{~cm}^{2}$.