In the following figure,

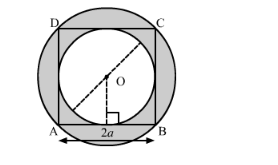
We have a square $\mathrm{ABCD}$ having $\mathrm{AB}=2 a$. From the given diagram we can observe that,

Radius of incircle $\left(r_{1}\right)=a$

Radius of circumcircle $\left(r_{2}\right)=\sqrt{2} a$

(i) We have to find the ratio of the circumferences of the two circles. So the required ratio is,

$=\frac{\text { Perimeter of inner circle }}{\text { Perimeter of circumcircle }}$

$=\frac{2 \pi(a)}{2 \pi(\sqrt{2} a)}$

$=\frac{1}{\sqrt{2}}$

(ii) We have to find the ratio of the areas of the two circles. So the required ratio is,

$=\frac{\text { Area of inner circle }}{\text { Area of circumcircle }}$

$=\frac{\pi(a)^{2}}{\pi(\sqrt{2} a)^{2}}$

$=\frac{1}{2}$