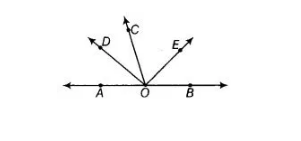
In the figure, OD is the bisector of ∠AOC, OE is the bisector of ∠BOC and OD ⊥ OE. Show that the points A, 0 and B are collinear.
Thinking Process
For showing collinearity of A, O and B, we have to show that ∠AOB =180°.
Given In the figure, OD ⊥ OE, OD and OE are the bisectors of ∠AOC and ∠BOC.
To show Points A, O and B are collinear i.e., AOB is a straight line.
Proof Since, OD and OE bisect angles ∠AOC and ∠BOC, respectively.
∠AOC =2 ∠DOC …(i)
and ∠COB = 2 ∠COE …(ii)
On adding Eqs. (i) and (ii), we get
∠AOC + ∠COB = 2 ∠DOC +2 ∠COE => ∠AOC +∠COB = 2(∠DOC +∠COE)
=> ∠AOC + ∠COB= 2 ∠DOE
=> ∠AOC+ ∠COB = 2 x 90° [∴ OD ⊥ OE]
=> ∠AOC + ∠COB = 180°
∴ ∠AOB = 180°
So, ∠AOC and ∠COB are forming linear pair.
Also, AOB is a straight line.
Hence, points A, O and B are collinear.
